I’ve been meaning to finish once and for all Knzhou’s Data and Uncertainty handout (P2), but the experimental problem I just keep putting off. Today was finally a break from deadlines, so let’s do it.

The problem:

Problem 22. The acceleration due to gravity can be measured by measuring the time period of a simple pendulum. However, it can be challenging to get an accurate result. (a) Suppose you constructed a pendulum using regular household materials. Name at least five sources of possible experimental error in your calculated value of g. How would you make the pendulum and perform the measurements to minimize these sources of error? (b) Make an actual pendulum yourself and carry out the measurement. Describe your experimental procedure and show your data. Estimate as many of the sources of experimental error identified in part (a) as you can, and using them, give a value of g with a reasonable uncertainty. (c) If you had $1,000 and a week to do plenty of measurements, how would you go about it? How precise a result do you think you could get? What would be the dominant sources of uncertainty remaining?

Theory

Let’s first quickly solve it analytically.

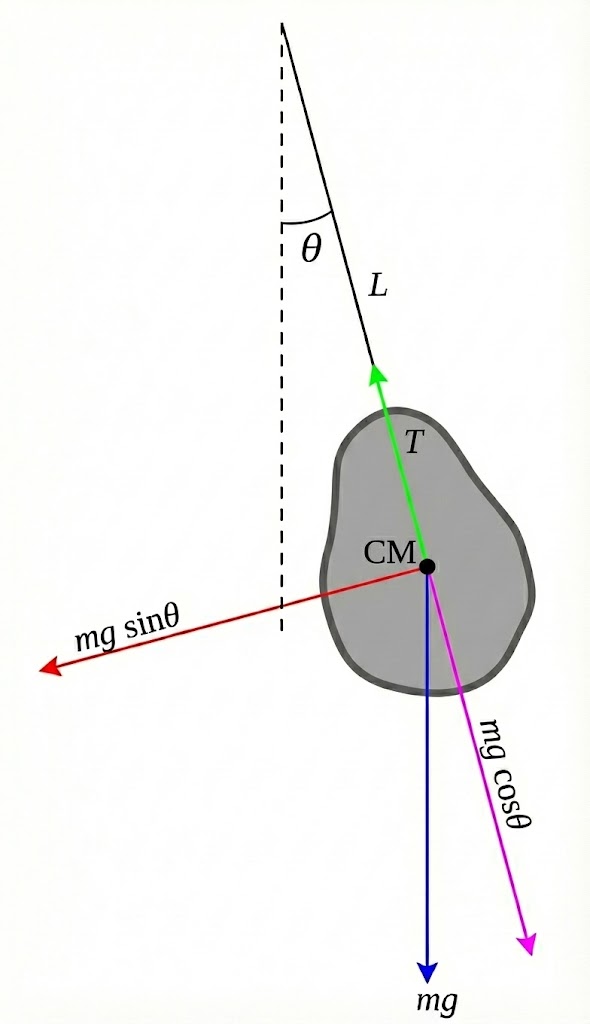
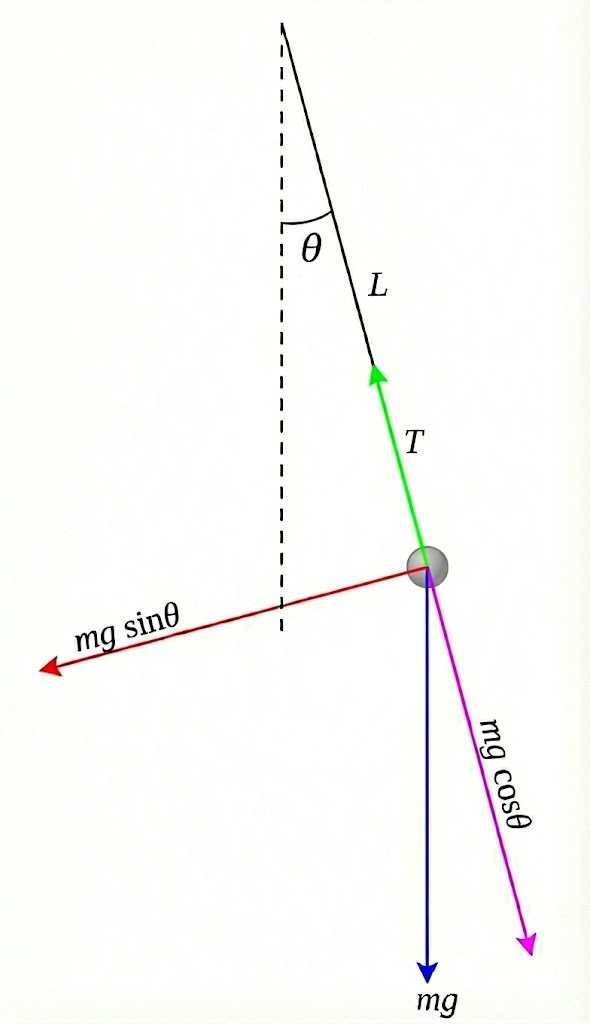
From the second law, we have

$$\tau=I\alpha$$ $$-mgL\sin\theta=I\frac{d^2\theta}{dt^2}$$

With small angle approximation ($\sin\theta\approx\theta$), this gives

$$-(mgL/I)\theta=\frac{d^2\theta}{dt^2}$$ $$\omega=\sqrt{\frac{mgL}{I}}$$

and since $T=2\pi/\omega$, the period is $T=2\pi\sqrt{\frac{I}{mgL}}$.

The problem says to use simple pendulum (point mass as the bob), so $I=mL^2$. Substituting, we get

$$T=2\pi\sqrt{\frac{L}{g}}$$

Now solve for $g$:

$$g=\boxed{\frac{4\pi^2L}{T^2}}$$

So all we need to do is measure the string’s length $L$ and the period $T$. Simple, right?

Attempt 1: Collecting data (running into reality)

The only materials we need are a string, a pendulum bob, and a stopwatch.

I didn’t have any ideal object with simple moment of inertia, so I thought I’d first try to just use a longer string and let the $d$ in $I=I_{cm}+md^2$ dominate.

And for the bob, I chose the densest thing around to remove the effect of string’s mass: my characte- jk I mean this lotion bottle.

I took 5 trials of 10 periods each (let nature do the summing to reduce uncertainty).

Trial	Time for 10 periods (s)	Period $T$ (s)
1	15.45	1.545
2	15.36	1.536
3	15.47	1.547
4	15.40	1.540
5	15.39	1.539
Average	15.414	1.5414

$$T=1.5414\text{ s}$$

I only had the edge of protractor as my ruler, and the bob was already tied up, so it was a real pain to measure $L$. It came out, after 3 back-to-back measurements, to be ~14 inches or 35.6 cm.

$$L=0.356\text{ m}$$

Substituting into the equation, we get.. *drumroll*

$$g=\frac{4\pi^2L}{T^2}=\frac{4\pi^2\times 0.356}{1.5414^2}=\boxed{5.925\text{ m/s}^2}$$

What??

Attempt 2: Debugging, irl

What could be wrong?

• Friction from the string: probably not much—10 oscillations don’t show noticeable damping
• Air drag: same as above, though drag would increase period, and $g\propto\frac{1}{T^2}$, which is in the direction of the error. hm.
• String’s mass: definitely negligible compared to the mass of the bob.
• Small angle approximation: angle was already very small.
• Lotion’s moment of inertia NOT a point mass <- this is probably it; $I_{CM}$ is still pretty large compared to $md^2$.
• L is too uncertain <- I need a better way to measure than back-to-back guesstimates.

Time for round two.

This time I marked string’s length exact with the edge of a sheet of paper (11 x 8.5in) and accounted for a little 0.5cm leftover when tying:

Also adding in an extra ~1cm from the string to the paperclip’s CM, we get

$$L=11\text{in}+0.5\text{cm}+1\text{cm}=0.2944\text{ m}$$

To get a smaller $I_{CM}$, I used a small binder clip on one end. Voila:

With some focused attention, I got 5 trials of 10 periods each:

Trial	Time for 10 periods (s)	Period $T$ (s)
1	11.07	1.107
2	11.07	1.107
3	11.12	1.112
4	11.10	1.110
5	11.16	1.116
Average	11.104	1.1104

Now do I just use the average period $T=1.1104\text{ s}$?

I tried playing the reaction time game a few times and found my delay to be ~0.2s. Since I start the stopwatch right as I let go, there’s no delay there. It’s not symmetric. Let’s subtract $0.2\text{ s}/10=0.02\text{ s}$ from the average:

$$T=1.1104\text{ s}-0.02\text{ s}=1.0904\text{ s}$$

Ok, but before we calculate the new $g$, let’s find its uncertainty.

Uncertainty analysis

How far off are we?

The uncertainty in $L$ is $\Delta L=0.01\text{ cm}=0.0001\text{ m}$. The uncertainty in $T$ is my reaction time of $\Delta T=0.2\text{ s}/10=0.02\text{ s}$.

$$\Delta g=4\pi^2 \times \Delta\left(LT^{-2}\right)$$

We can write $LT^{-2}$ as $\exp\left(\ln(L)+\ln(T^{-2})\right)$ and repeatedly apply $\Delta (f(x))\approx |f'(x)|\Delta x$, like a chain rule.

$$\Delta g=4\pi^2 \times \Delta\left(LT^{-2}\right)=4\pi^2 \times LT^{-2}\sqrt{\left(\frac{\Delta L}{L}\right)^2+\left(\frac{-2\Delta T}{T}\right)^2}=0.016\text{ m/s}^2$$

Results

Putting all that together…

$$g=\frac{4\pi^2L}{T^2}=\frac{4\pi^2\times 0.2944}{1.0904^2}=\boxed{9.7752\pm 0.016\text{ m/s}^2}$$

haHA. It worked!! It doesn’t exactly contain $g=9.805\text{ m/s}^2$, but pretty close I’d say.

(maybe things are just further from Earth’s core where I live :P)

Wow now I realize it’s been so long since I’ve built something physical. I’ve become addicted to reading new theory, and gotten too used to just manipulating equations and imagining on paper, I’d forgotten how fun it is to actually get outside and poke reality. To finally see with my own eyes these measurements actually work out.

Wizardry, I tell you!

**

I’m really glad I finally decided to complete the experimental problem. Though another part of me wonders how much skill I actually learned from a simple exercise like this. Was it really productive or just indulgent pleasure? Honestly, I could keep doing this for days…